vault backup: 2023-11-08 22:20:40
This commit is contained in:
parent
a6868a3294
commit
4210d543af
@ -61,6 +61,20 @@ $$p \rightarrow q\cdot p \cdot q^-1$$
|
|||||||
## 四元数规范化
|
## 四元数规范化
|
||||||
$$x^2 + y^2 + z^2 =1$$
|
$$x^2 + y^2 + z^2 =1$$
|
||||||
|
|
||||||
|
## 四元数乘法
|
||||||
|
$$q_1q_2=(a+bi+cj+dk)(e+fi+gi+hk)$$
|
||||||
|
<EFBFBD>1<EFBFBD>2=(<28>+<2B><>+<2B><>+<2B><>)(<28>+<2B><>+<2B><>+ℎ<>)
|
||||||
|
|
||||||
|
<EFBFBD>1<EFBFBD>2=<3D><>+<2B><><EFBFBD>+<2B><><EFBFBD>+<2B>ℎ<EFBFBD>+<2B><><EFBFBD>+<2B><><EFBFBD>2+<2B><><EFBFBD><EFBFBD>+<2B>ℎ<EFBFBD><E2848E>+<2B><><EFBFBD>+<2B><><EFBFBD><EFBFBD>+<2B><><EFBFBD>2+<2B>ℎ<EFBFBD><E2848E>+<2B><><EFBFBD>+<2B><><EFBFBD><EFBFBD>+<2B><><EFBFBD><EFBFBD>+<2B>ℎ<EFBFBD>2
|
||||||
|
|
||||||
|
使用 <EFBFBD>2=<3D>2=<3D>2=<3D><><EFBFBD>=−1 化简上述等式
|
||||||
|
|
||||||
|
<EFBFBD>1<EFBFBD>2=(<28><>−<EFBFBD><E28892>−<EFBFBD><E28892>−<EFBFBD>ℎ)+......(<28><>+<2B><>−<EFBFBD><E28892>+<2B>ℎ)<29>+.......(<28><>+<2B><>+<2B><>−<EFBFBD>ℎ)<29>+......(<28><>−<EFBFBD><E28892>+<2B><>+<2B>ℎ)<29>
|
||||||
|
|
||||||
|
可以看到前面的系数可以写成一个矩阵
|
||||||
|
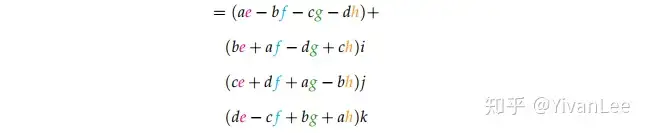
|
||||||
|
|
||||||
|
所以可以得到矩阵形式
|
||||||
## 四元数求反
|
## 四元数求反
|
||||||
```c++
|
```c++
|
||||||
inline QQuaternion QQuaternion::inverted() const
|
inline QQuaternion QQuaternion::inverted() const
|
||||||
@ -77,6 +91,11 @@ inline QQuaternion QQuaternion::inverted() const
|
|||||||
}
|
}
|
||||||
```
|
```
|
||||||
|
|
||||||
|
## 四元数复合旋转
|
||||||
|
$$q_{next}=q_2q_1$$
|
||||||
|
$$v'=q_2q_1vq_1^*q_2^*$$
|
||||||
|
`q*`为反函数。
|
||||||
|
|
||||||
# FBX
|
# FBX
|
||||||
四元数旋转顺序 xyz
|
四元数旋转顺序 xyz
|
||||||
可以使用
|
可以使用
|
||||||
|
|||||||
Loading…
x
Reference in New Issue
Block a user