115 lines
4.1 KiB
Markdown
115 lines
4.1 KiB
Markdown
---
|
||
title: 四元数学习笔记
|
||
date: 2023-10-25 13:16:32
|
||
excerpt:
|
||
tags:
|
||
rating: ⭐
|
||
---
|
||
|
||
# 前言
|
||
推荐学习视频:
|
||
- [四元数的可视化](https://www.bilibili.com/video/BV1SW411y7W1/?spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=d47c0bb42f9c72fd7d74562185cee290)
|
||
- [四元数和三维转动,可互动的探索式视频](https://www.bilibili.com/video/BV14Y4y1z7xW/?spm_id_from=333.788.recommend_more_video.1&vd_source=d47c0bb42f9c72fd7d74562185cee290)
|
||
|
||
另外作者还建立了一个四元数可视化网站: https://eater.net/quaternions ,点击里面的教学视频之后点击正方上的按钮就可以停止播放视频,并且可以手动操作四元数。
|
||
|
||
# 四元数
|
||
是一个四维数值系统用于描述三维空间关系。(现在主要用于描述旋转)
|
||
|
||
四元数的表达形式为:
|
||
$$q = w + xi + yj +zk$$
|
||
|
||
ijk可以分别理解为使用虚数来表示x、y、z3个轴的旋转值,使用一个实数w作为Scale。
|
||
本身就可以理解为球形角度映射到一根轴上。举例:假设在二维坐标轴中,i,j即为x,y轴的坐标值。扩展到三维即i,j,k为x,y,z的坐标值。
|
||
|
||
## 四元数与旋转矩阵
|
||
图中的绿色、红色、蓝色部分分别是四元数的i j k的数据。
|
||

|
||
|
||
|
||
|
||
# 计算规则
|
||
四元数可用一般分配率来计算,其虚部遵循以下规则:
|
||
$$i^2+j^2+k^2=-1$$
|
||
$$ij = -ji =k$$
|
||
$$jk=-ky=i$$
|
||
$$ki=-ik=j$$
|
||
|
||
# 旋转规则
|
||
以垂直关系依次旋转每个轴。
|
||
|
||
## 右手定理
|
||
>视频作者为了方便理解创建出的理论。当i的数值从0=>i时,垂直于x轴的yz平面就会按照右手方向(逆时针)进行旋转。
|
||
|
||
PS.该定理是建立在使用左乘规则的基础上,如果使用右乘,就需要变成左手定理。
|
||
|
||
## 左乘规则
|
||
$$q \cdot p$$
|
||
可以看做为使用四元数q对点P进行了旋转。
|
||
所以四元数乘法不满足交换律。
|
||
$$q \cdot p \neq p \cdot q$$
|
||
|
||
右乘规则顺序相反。
|
||
|
||
|
||
# 在3D世界中使用四元数来控制旋转
|
||
使用四元数将物体旋转,需要使用到"夹心乘法"
|
||
$$p \rightarrow q\cdot p \cdot q^-1$$
|
||
|
||

|
||
|
||
## 四元数规范化
|
||
$$x^2 + y^2 + z^2 =1$$
|
||
|
||
## 四元数乘法
|
||
$$q_1q_2=(a+bi+cj+dk)(e+fi+gi+hk)$$
|
||
<EFBFBD>1<EFBFBD>2=(<28>+<2B><>+<2B><>+<2B><>)(<28>+<2B><>+<2B><>+ℎ<>)
|
||
|
||
<EFBFBD>1<EFBFBD>2=<3D><>+<2B><><EFBFBD>+<2B><><EFBFBD>+<2B>ℎ<EFBFBD>+<2B><><EFBFBD>+<2B><><EFBFBD>2+<2B><><EFBFBD><EFBFBD>+<2B>ℎ<EFBFBD><E2848E>+<2B><><EFBFBD>+<2B><><EFBFBD><EFBFBD>+<2B><><EFBFBD>2+<2B>ℎ<EFBFBD><E2848E>+<2B><><EFBFBD>+<2B><><EFBFBD><EFBFBD>+<2B><><EFBFBD><EFBFBD>+<2B>ℎ<EFBFBD>2
|
||
|
||
使用 <EFBFBD>2=<3D>2=<3D>2=<3D><><EFBFBD>=−1 化简上述等式
|
||
|
||
<EFBFBD>1<EFBFBD>2=(<28><>−<EFBFBD><E28892>−<EFBFBD><E28892>−<EFBFBD>ℎ)+......(<28><>+<2B><>−<EFBFBD><E28892>+<2B>ℎ)<29>+.......(<28><>+<2B><>+<2B><>−<EFBFBD>ℎ)<29>+......(<28><>−<EFBFBD><E28892>+<2B><>+<2B>ℎ)<29>
|
||
|
||
可以看到前面的系数可以写成一个矩阵
|
||
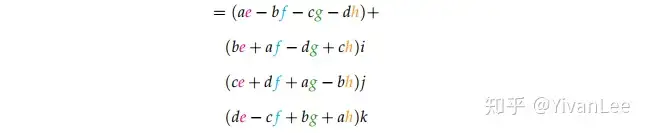
|
||
|
||
所以可以得到矩阵形式
|
||
## 四元数求反
|
||
```c++
|
||
inline QQuaternion QQuaternion::inverted() const
|
||
{
|
||
// Need some extra precision if the length is very small.
|
||
double len = double(wp) * double(wp) +
|
||
double(xp) * double(xp) +
|
||
double(yp) * double(yp) +
|
||
double(zp) * double(zp);
|
||
if (!qFuzzyIsNull(len))
|
||
return QQuaternion(float(double(wp) / len), float(double(-xp) / len),
|
||
float(double(-yp) / len), float(double(-zp) / len));
|
||
return QQuaternion(0.0f, 0.0f, 0.0f, 0.0f);
|
||
}
|
||
```
|
||
|
||
## 四元数复合旋转
|
||
$$q_{next}=q_2q_1$$
|
||
$$v'=q_2q_1vq_1^*q_2^*$$
|
||
`q*`为反函数。
|
||
|
||
# FBX
|
||
四元数旋转顺序 xyz
|
||
可以使用
|
||
`FbxNode::RotationOrder`
|
||
了解其顺序。
|
||
|
||
旋转xyz分别为
|
||
the "roll" about the x-axis along the plane,
|
||
the "pitch" about the y-axis which extends along the wings of the plane,
|
||
and the "yaw" or "heading" about the z-axis
|
||
|
||
# Qt
|
||
Qt中四元数旋转顺序zyx 或 yxz
|
||
旋转xyz分别为pitch yaw roll
|
||
|
||
# UE
|
||
UE中四元数的旋转顺序为**zyx**。其中旋转X轴为Roll,旋转Y轴为Pitch,旋转Z轴为Yaw |