322 lines
11 KiB
Markdown
322 lines
11 KiB
Markdown
---
|
||
title: 四元数学习笔记
|
||
date: 2023-10-25 13:16:32
|
||
excerpt:
|
||
tags:
|
||
rating: ⭐
|
||
---
|
||
|
||
# 前言
|
||
- 学习视频:
|
||
- [四元数的可视化](https://www.bilibili.com/video/BV1SW411y7W1/?spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=d47c0bb42f9c72fd7d74562185cee290)
|
||
- [四元数和三维转动,可互动的探索式视频](https://www.bilibili.com/video/BV14Y4y1z7xW/?spm_id_from=333.788.recommend_more_video.1&vd_source=d47c0bb42f9c72fd7d74562185cee290)
|
||
- 文章:
|
||
- https://zhuanlan.zhihu.com/p/104288667
|
||
- https://zhuanlan.zhihu.com/p/442146306
|
||
|
||
另外作者还建立了一个四元数可视化网站: https://eater.net/quaternions ,点击里面的教学视频之后点击正方上的按钮就可以停止播放视频,并且可以手动操作四元数。
|
||
|
||
# 四元数
|
||
是一个四维数值系统用于描述三维空间关系。(现在主要用于描述旋转)
|
||
|
||
四元数的表达形式为:
|
||
$$q = w + xi + yj +zk$$
|
||
|
||
ijk可以分别理解为使用虚数来表示x、y、z3个轴的旋转值,使用一个实数w作为Scale。
|
||
本身就可以理解为球形角度映射到一根轴上。举例:假设在二维坐标轴中,i,j即为x,y轴的坐标值。扩展到三维即i,j,k为x,y,z的坐标值。
|
||
|
||
## 四元数与旋转矩阵
|
||
图中的绿色、红色、蓝色部分分别是四元数的i j k的数据。
|
||

|
||
|
||
|
||
|
||
# 计算规则
|
||
四元数可用一般分配率来计算,其虚部遵循以下规则:
|
||
$$i^2+j^2+k^2=-1$$
|
||
$$ij = -ji =k$$
|
||
$$jk=-ky=i$$
|
||
$$ki=-ik=j$$
|
||
|
||
# 旋转规则
|
||
以垂直关系依次旋转每个轴。
|
||
|
||
## 右手定理
|
||
>视频作者为了方便理解创建出的理论。当i的数值从0=>i时,垂直于x轴的yz平面就会按照右手方向(逆时针)进行旋转。
|
||
|
||
PS.该定理是建立在使用左乘规则的基础上,如果使用右乘,就需要变成左手定理。
|
||
|
||
## 左乘规则
|
||
$$q \cdot p$$
|
||
可以看做为使用四元数q对点P进行了旋转。
|
||
所以四元数乘法不满足交换律。
|
||
$$q \cdot p \neq p \cdot q$$
|
||
|
||
右乘规则顺序相反。
|
||
|
||
|
||
# 在3D世界中使用四元数来控制旋转
|
||
使用四元数将物体旋转,需要使用到"夹心乘法"
|
||
$$p \rightarrow q\cdot p \cdot q^-1$$
|
||
|
||

|
||
|
||
## 四元数规范化
|
||
$$x^2 + y^2 + z^2 =1$$
|
||
|
||
## 四元数乘法
|
||
$$q_1q_2=(a+bi+cj+dk)(e+fi+gi+hk)$$
|
||
<EFBFBD>1<EFBFBD>2=(<28>+<2B><>+<2B><>+<2B><>)(<28>+<2B><>+<2B><>+ℎ<>)
|
||
|
||
<EFBFBD>1<EFBFBD>2=<3D><>+<2B><><EFBFBD>+<2B><><EFBFBD>+<2B>ℎ<EFBFBD>+<2B><><EFBFBD>+<2B><><EFBFBD>2+<2B><><EFBFBD><EFBFBD>+<2B>ℎ<EFBFBD><E2848E>+<2B><><EFBFBD>+<2B><><EFBFBD><EFBFBD>+<2B><><EFBFBD>2+<2B>ℎ<EFBFBD><E2848E>+<2B><><EFBFBD>+<2B><><EFBFBD><EFBFBD>+<2B><><EFBFBD><EFBFBD>+<2B>ℎ<EFBFBD>2
|
||
|
||
使用 <EFBFBD>2=<3D>2=<3D>2=<3D><><EFBFBD>=−1 化简上述等式
|
||
|
||
<EFBFBD>1<EFBFBD>2=(<28><>−<EFBFBD><E28892>−<EFBFBD><E28892>−<EFBFBD>ℎ)+......(<28><>+<2B><>−<EFBFBD><E28892>+<2B>ℎ)<29>+.......(<28><>+<2B><>+<2B><>−<EFBFBD>ℎ)<29>+......(<28><>−<EFBFBD><E28892>+<2B><>+<2B>ℎ)<29>
|
||
|
||
可以看到前面的系数可以写成一个矩阵
|
||
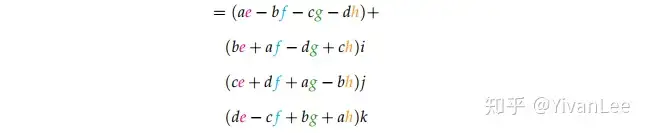
|
||
|
||
所以可以得到矩阵形式
|
||
## 四元数求反
|
||
```c++
|
||
inline QQuaternion QQuaternion::inverted() const
|
||
{
|
||
// Need some extra precision if the length is very small.
|
||
double len = double(wp) * double(wp) +
|
||
double(xp) * double(xp) +
|
||
double(yp) * double(yp) +
|
||
double(zp) * double(zp);
|
||
if (!qFuzzyIsNull(len))
|
||
return QQuaternion(float(double(wp) / len), float(double(-xp) / len),
|
||
float(double(-yp) / len), float(double(-zp) / len));
|
||
return QQuaternion(0.0f, 0.0f, 0.0f, 0.0f);
|
||
}
|
||
```
|
||
|
||
## 四元数复合旋转
|
||
$$q_{next}=q_2q_1$$
|
||
$$v'=q_2q_1vq_1^*q_2^*$$
|
||
可以通过推导以及模长等效计算的方式得出。以下假设r为单位四元数:
|
||
$$p'=p{\parallel}+rp{\perp}= 1 \cdot p{\parallel} + rp{\perp}=qq^{-1} p{\parallel}+qqp{\perp}=qp{\parallel}q^*+qp{\perp}q^*=q(p{\parallel}+p{\perp})q^*$$
|
||
|
||
因为$$p=p{\parallel}+p{\perp}$$
|
||
所以$$p'=qpq^*$$
|
||
## 共轭四元数与求反
|
||
对于模长为1的单位四元数,我们可以写成:
|
||
$$q^*=q^{-1}$$
|
||
`q*`为共轭四元数。共轭四元数可以通过对四元数的向量部分求反来计算:
|
||
$$q=[s,v]$$
|
||
$$q^*=[s,-v]$$
|
||
## 四元数与欧拉数转换
|
||
>**为什么实际旋转角度是四元数里面的角度的两倍?有什么数学上的原因吗?**
|
||
- https://www.zhihu.com/question/41485992/answer/91194777
|
||
- 这个回答比较直观:https://www.zhihu.com/question/41485992/answer/776988632
|
||
|
||
> 主要原因是,普通三维空间,若矢量是r,旋转变换矩阵是S,那么矢量变成 Sr 。即矢量的变换,是用变换矩阵直接乘。
|
||
而四元数空间中,对应的形式,是需要两边乘的,即 qpq^(-1) , 所以,对于旋转,右边的乘法旋转θ/2角, 左边的乘法旋转θ/2角,才能对应普通三维空间旋转θ角.
|
||
那么,为什么是qpq^(-1)的形式? 因为四元数空间中谈三维空间中的旋转,必须把四元数r(任意的)先旋转到实分量为0的分空间中,即 xi+yj+zk空间中。所以,p不是矢量,而是对矢量r的变换。 而q是个表象变换(这里是坐标系的某种旋转)。 qpq^(-1)就是表象变换后,p变换的形式。
|
||
|
||
推荐参考[matthew-brett/transforms3d](https://github.com/matthew-brett/transforms3d/blob/main/transforms3d/euler.py)。以下是本人的移植c++版本:
|
||
```c++
|
||
/*
|
||
* 移植Python的Transform3D库内容
|
||
*/
|
||
// axis sequences for Euler angles
|
||
QVector<int> _NEXT_AXIS{1, 2, 0, 1};
|
||
|
||
QMap<QString,QVector<int>> _AXES2TUPLE{
|
||
{QString("sxyz"), {0, 0, 0, 0}}, {QString("sxyx"), {0, 0, 1, 0}}, {QString("sxzy"), {0, 1, 0, 0}},
|
||
{QString("sxzx"), {0, 1, 1, 0}}, {QString("syzx"), {1, 0, 0, 0}}, {QString("syzy"), {1, 0, 1, 0}},
|
||
{QString("syxz"), {1, 1, 0, 0}}, {QString("syxy"), {1, 1, 1, 0}}, {QString("szxy"), {2, 0, 0, 0}},
|
||
{QString("szxz"), {2, 0, 1, 0}}, {QString("szyx"), {2, 1, 0, 0}}, {QString("szyz"), {2, 1, 1, 0}}
|
||
};
|
||
|
||
QMap<QVector<int>,QString> _TUPLE2AXES{
|
||
{{0, 0, 0, 0},QString("sxyz")}, {{0, 0, 1, 0},QString("sxyx")}, {{0, 1, 0, 0},QString("sxzy")},
|
||
{{0, 1, 1, 0},QString("sxzx")}, {{1, 0, 0, 0},QString("syzx")}, {{1, 0, 1, 0},QString("syzy")},
|
||
{{1, 1, 0, 0},QString("syxz")}, {{1, 1, 1, 0},QString("syxy")}, {{2, 0, 0, 0},QString("szxy")},
|
||
{{2, 0, 1, 0},QString("szxz")}, {{2, 1, 0, 0},QString("szyx")}, {{2, 1, 1, 0},QString("szyz")}
|
||
};
|
||
|
||
// For testing whether a number is close to zero
|
||
double _EPS4 = std::numeric_limits<double>::epsilon() * 4.0;
|
||
|
||
QVector<QVector<double>> quat2mat(Quaternion q)
|
||
{
|
||
double w = q.w;
|
||
double x = q.x;
|
||
double y = q.y;
|
||
double z = q.z;
|
||
|
||
double Nq = w*w + x*x + y*y + z*z;
|
||
if (Nq < std::numeric_limits<double>::epsilon())
|
||
return {{1.0,0.0,0.0},
|
||
{0.0,1.0,0.0},
|
||
{0.0,0.0,1.0}};
|
||
|
||
double s = 2.0/Nq;
|
||
double X = x*s;
|
||
double Y = y*s;
|
||
double Z = z*s;
|
||
double wX = w*X;double wY = w*Y;double wZ = w*Z;
|
||
double xX = x*X;double xY = x*Y;double xZ = x*Z;
|
||
double yY = y*Y;double yZ = y*Z;double zZ = z*Z;
|
||
return {{ 1.0-(yY+zZ), xY-wZ, xZ+wY },
|
||
{ xY+wZ, 1.0-(xX+zZ), yZ-wX },
|
||
{ xZ-wY, yZ+wX, 1.0-(xX+yY) }};
|
||
}
|
||
|
||
QVector<double> mat2euler(QVector<QVector<double>> mat,const QString& axesStr)
|
||
{
|
||
const QVector<int> AXES=_AXES2TUPLE[axesStr];
|
||
int firstaxis = AXES[0];
|
||
int parity = AXES[1];
|
||
int repetition = AXES[2];
|
||
int frame = AXES[3];
|
||
|
||
int i = firstaxis;
|
||
int j = _NEXT_AXIS[i+parity];
|
||
int k = _NEXT_AXIS[i-parity+1];
|
||
|
||
QVector<QVector<double>> M = mat;
|
||
|
||
double ax,ay,az;
|
||
if(repetition){
|
||
double sy = qSqrt(M[i][j]*M[i][j] + M[i][k]*M[i][k]);
|
||
if(sy > _EPS4){
|
||
ax = qAtan2( M[i][j], M[i][k]);
|
||
ay = qAtan2( sy, M[i][i]);
|
||
az = qAtan2( M[j][i], -M[k][i]);
|
||
}else{
|
||
ax = qAtan2(-M[j][k], M[j][j]);
|
||
ay = qAtan2( sy, M[i][i]);
|
||
az = 0.0;
|
||
}
|
||
}else{
|
||
double cy = qSqrt(M[i][i]*M[i][i] + M[j][i]*M[j][i]);
|
||
if(cy > _EPS4){
|
||
ax = qAtan2( M[k][j], M[k][k]);
|
||
ay = qAtan2(-M[k][i], cy);
|
||
az = qAtan2( M[j][i], M[i][i]);
|
||
}else{
|
||
ax = qAtan2(-M[j][k], M[j][j]);
|
||
ay = qAtan2(-M[k][i], cy);
|
||
az = 0.0;
|
||
}
|
||
}
|
||
|
||
if(parity){
|
||
ax = -ax;
|
||
ay = -ay;
|
||
az = -az;
|
||
}
|
||
if (frame){
|
||
std::swap(ax,az);
|
||
}
|
||
|
||
return {qRadiansToDegrees(ax), qRadiansToDegrees(ay), qRadiansToDegrees(az)};
|
||
}
|
||
|
||
Quaternion euler2quat(double ai,double aj,double ak,const QString& axesStr)
|
||
{
|
||
ai = qDegreesToRadians(ai);
|
||
aj = qDegreesToRadians(aj);
|
||
ak = qDegreesToRadians(ak);
|
||
|
||
const QVector<int> AXES=_AXES2TUPLE[axesStr];
|
||
int firstaxis = AXES[0];
|
||
int parity = AXES[1];
|
||
int repetition = AXES[2];
|
||
int frame = AXES[3];
|
||
|
||
int i = firstaxis + 1;
|
||
int j = _NEXT_AXIS[i+parity-1] + 1;
|
||
int k = _NEXT_AXIS[i-parity] + 1;
|
||
|
||
if(frame)
|
||
{
|
||
std::swap(ak,ai);
|
||
}
|
||
|
||
if(parity)
|
||
{
|
||
aj= -aj;
|
||
}
|
||
|
||
ai = ai / 2.0;
|
||
aj = aj / 2.0;
|
||
ak = ak / 2.0;
|
||
|
||
double ci = qCos(ai);
|
||
double si = qSin(ai);
|
||
double cj = qCos(aj);
|
||
double sj = qSin(aj);
|
||
double ck = qCos(ak);
|
||
double sk = qSin(ak);
|
||
double cc = ci * ck;
|
||
double cs = ci * sk;
|
||
double sc = si * ck;
|
||
double ss = si * sk;
|
||
|
||
QVector<double> q(4);
|
||
if (repetition)
|
||
{
|
||
q[0] = cj*(cc - ss);
|
||
q[i] = cj*(cs + sc);
|
||
q[j] = sj*(cc + ss);
|
||
q[k] = sj*(cs - sc);
|
||
}
|
||
else
|
||
{
|
||
q[0] = cj*cc + sj*ss;
|
||
q[i] = cj*sc - sj*cs;
|
||
q[j] = cj*ss + sj*cc;
|
||
q[k] = cj*cs - sj*sc;
|
||
}
|
||
|
||
if(parity)
|
||
{
|
||
q[j] *= -1.0;
|
||
}
|
||
|
||
return Quaternion{q[0],q[1],q[2],q[3]};
|
||
}
|
||
|
||
QQuaternion euler2quaternion(double ai,double aj,double ak,const QString& axesStr)
|
||
{
|
||
const Quaternion& q = euler2quat(ai,aj,ak,axesStr);
|
||
return QQuaternion(q.w,q.x,q.y,q.z);
|
||
}
|
||
|
||
QVector<double> quat2euler(Quaternion quaternion,const QString& axes)
|
||
{
|
||
return mat2euler(quat2mat(quaternion), axes);
|
||
}
|
||
|
||
QVector3D quaternion2euler(QQuaternion quaternion,const QString& axes)
|
||
{
|
||
const QVector4D Vec=quaternion.toVector4D();
|
||
Quaternion q{Vec.w(),Vec.x(),Vec.y(),Vec.z()};
|
||
const QVector<double>& Euler = quat2euler(q,axes);
|
||
return QVector3D(Euler[0],Euler[1],Euler[2]);
|
||
}
|
||
```
|
||
|
||
# FBX
|
||
四元数旋转顺序 xyz
|
||
可以使用
|
||
`FbxNode::RotationOrder`
|
||
了解其顺序。
|
||
|
||
旋转xyz分别为
|
||
the "roll" about the x-axis along the plane,
|
||
the "pitch" about the y-axis which extends along the wings of the plane,
|
||
and the "yaw" or "heading" about the z-axis
|
||
|
||
# Qt
|
||
Qt中四元数旋转顺序zyx 或 yxz
|
||
旋转xyz分别为pitch yaw roll
|
||
|
||
# UE
|
||
UE中四元数的旋转顺序为**zyx**。其中旋转X轴为Roll,旋转Y轴为Pitch,旋转Z轴为Yaw |